Nessa publicação iremos demonstrar a Lei de Reflexão Mecânica que é dada por $e=\frac{\tan{i}-\mu}{\tan{r}+\mu}$, onde $e$ é o coeficiente de restituição mecânica, $i$ é o ângulo de incidência, $r$ é o ângulo de reflexão e $\mu$ é o coeficiente de atrito.
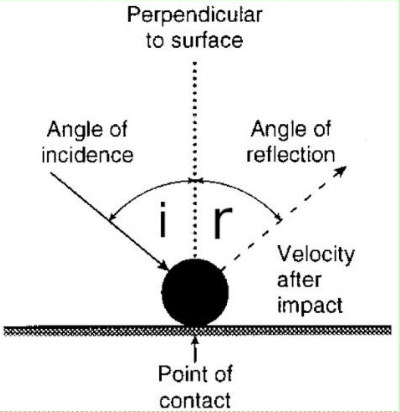
Inicialmente, analisando o eixo X, temos:
$$I_{res_{x}}=mv’\sin{r}-mv\sin{i}=-F_{at_{méd}}\Delta{t}=-{\mu}N_{méd}\Delta{t}$$
$${mv’\sin{r}-mv\sin{i}=-{\mu}N_{méd}\Delta{t}}\:(i)$$
Analisando o eixo Y, temos:
$$e=\frac{v’\cos{r}}{v\cos{i}}$$
$$ev\cos{i}=v’\cos{r}\:(ii)$$
$$I_{res_{y}}=mv’\cos{r}-(-mv\cos{i})=N_{méd}\Delta{t}$$
$$mv’\cos{r}+mv\cos{i}=N_{méd}\Delta{t}\:(iii)$$
Dividindo $(i)$ por $(ii)$:
$$\frac{mv’\sin{r}-mv\sin{i}}{mv’\cos{r}+mv\cos{i}}=\frac{-{\mu}N_{méd}\Delta{t}}{N_{méd}\Delta{t}}$$
$$-{\mu}(v’\cos{r}+v\cos{i})=v’\sin{r}-v\sin{i}$$
$$(\sin{i}-{\mu}\cos{i})v=(\sin{r}+{\mu}\cos{r})v’\:(iv)$$
Dividindo $(iv)$ por $(ii)$:
$$\frac{(\sin{i}-{\mu}\cos{i})v}{ev\cos{i}}=\frac{(\sin{r}+{\mu}\cos{r})v’}{v’\cos{r}}$$
$$\tan{i}-{\mu}=(\tan{r}+{\mu})e$$
$${e=\frac{\tan{i}-\mu}{\tan{r}+\mu}}_{\:\blacksquare}$$
Lembrem-se: Entender, Praticar, Aprender, Repetir
Bons estudos!
Prof Ludwig B Sales
